论文阅读-自注意力GAN_SAGAN
时隔将近两个月,今天终于有机会又来写一篇啦~~
本次带来的是上次论文阅读-谱归一化_SN-GANs就说要写的自注意力机制
的对抗生成网络:SAGAN~~
1. 前情提要
众所周知,自从注意力机制被提出,就几乎成为了需要全局感知的模型标配了~~然而敏锐的作者发现:self-attention 还没有被用到GAN上!
对于GAN来说,其生成图像时大部分都是用的卷积操作,而卷积操作囿于其局部感受野,成也萧何败也萧何,所生成的图像不能很好地处理长距离依赖(long range
dependencies),于是作者便顺势提出了self-attention GAN~~
2. 何方神圣
先来张效果图感受一下:

图中,每行第一张图分别标记了 5 个典型的查询点,其后 5 张图分别是各个点对应的 attention map,箭头是其大致趋势。
可以看到,确实每个点的 attention 都在语义上较为相关的地方,果然还是有点意思~~
那么这个 self-attention 到底是咋做的?再来张图:
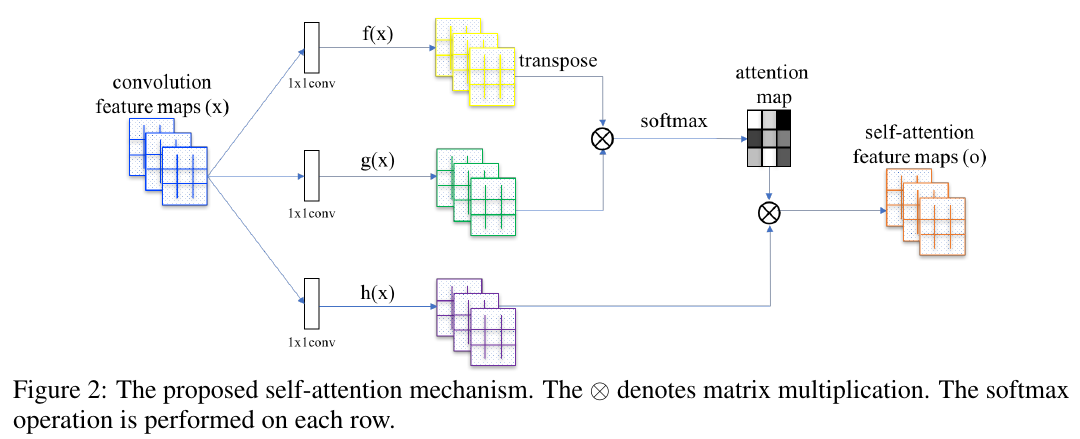
图中,我们取某一层的 feature map \(x\in\mathbb{R}^{C*N}\),然后有:
\[\begin{cases} & f(x)=W_fx\\ & g(x)=W_gx\\ & h(x)=W_hx \end{cases}\]式中,\(W_f\in\mathbb{R}^{\bar{C}*C}\),\(W_g\in\mathbb{R}^{\bar{C}*C}\),\(W_h\in\mathbb{R}^{C*C}\),于是,我们便知
\[\begin{cases} & f(x)\in\mathbb{R}^{\bar{C}*N}\\ & g(x)\in\mathbb{R}^{\bar{C}*N}\\ & h(x)\in\mathbb{R}^{C*N} \end{cases}\]然后我们计算:
\[s_{ij} = f(x_i)^Tg(x_j)\]可知 \(s\in \mathbb{R}^{N*N}\)。再令:
\[\beta_{j,i}=\frac{exp(s_ij)}{\sum_{i=1}^Nexp(s_{ij})}\]于是又有 \(\beta\in \mathbb{R}^{N*N}\)。
算到这里,其实 $\beta$ 已经是我们的注意力系数矩阵了。
将 $\beta$ 与 $h_x$ 相乘:
前面我们算到\(h(x)\in\mathbb{R}^{C*N}\),于是\(h(x)=(h(x_1),h(x_2),...,h(x_N))\),则有
\[h(x_i)\in\mathbb{R}^{C}\]同样的,则\(o_j\in\mathbb{R}^{C}\),\(o=(o_1,o_2,...,o_N)\),于是乎我们有:
\[o\in\mathbb{R}^{C*N}\]$o$ 即是我们的注意力层了(self-attention feature map)~
当然,作者还不失机智地加了个类似残差的结构来使训练更稳定:
\[y_i=\gamma o_i + x_i\]$\gamma$ 初始化为 0,训练中更新~~
3. 雕虫小技
众所周知,GAN也饱受训练过程不稳定的苦~
于是作者为此用了两个小技巧:
3.1 谱归一化
啥是谱归一化(Spectral normalization)?
我已经在我的上一篇博客:论文阅读-谱归一化_SN-GANs里详细阐述了,一句话总结就是:
谱归一化约束,通过约束 GAN 的 Discriminator 的每一层网络的权重矩阵(weight matrix)的谱范数来约束 Discriminator 的 Lipschitz 常数, 从而增强 GAN 在训练过程中的稳定性。
是不是被绕晕了?不用怕,点击我的上一篇博客看一遍,你应该会有一种豁然开朗的感觉~
传送门:论文阅读-谱归一化_SN-GANs
3.2 不同学习率
这个应该很好理解了,就是异步更新。
作者说 Discriminator 的约束拖慢了GAN的学习过程,于是乎借鉴 TTUR 的方法来在相同的时间内生成更好的结果。
4. 顾盼生姿
来张图秀一下:

如开头的那张图所示,看得出来确实每个点的 attention 都在语义上较为相关的地方,果然还是有点意思~~
微信公众号:璇珠杂俎(也可搜索oukohou),提供本站优质非技术博文~~

regards.
oukohou.
既已览卷至此,何不品评一二: